Spin 1/2 Particle on a Cylinder with

Radial Magnetic Field

C. Chryssomalakos,
ICN, UNAM, Mexico

A. Franco, and A. Reyes-Coronado
IF, UNAM, Mexico

This page was created as a complement to the homonymous article, published in the European Journal of Physics 25, 489-502 (2004). We collect here related visual material, still images and animations, as an aid in developing intuition about the system studied - it could also be of use in a classroom presentation.

Consider first a classical charged particle on a cylinder, in the presence of a radial magnetic field. Its motion consists of two oscillations, one along the axis z of the cylinder and one in the angular direction phi --- a typical orbit appears below.

Now consider the analogous problem in the quantum case. Schroedinger's equation separates, so that the wavefunction factorises into a function of z times a function of phi. It is shown in the above article that when the angular part of the wavefunction is exp(i k phi), the resulting equation for the z part reduces to that of a simple harmonic oscillator, whose quadratic potential is centered at z=-k b. Here b is a constant with dimensions of length built out of the parameters of the problem (radius of the cylinder, magnetic field strength etc.).

In the images and animations that follow, the modulus of the wavefunction is proportional to the radial distance between the gaussian and the cylinder, while its phase is color-coded by superimposing the color wheel on the left on the complex plane where the wavefunction takes values (positive reals are shown as red, positive pure imaginaries as green etc.).

What happens if we put the particle in an initial state represented by a gaussian (in z), centered at the origin, with exp(i k phi) as angular part? Then the particle "feels" a quadratic potential centered at z=-k b and the above initial state is a coherent state: time evolution consists in the oscillation of the gaussian around the center of the potential (i.e., from z=0 to z=-2kb) with the frequency of the oscillator.

Now consider the same initial state as above in z, but with a -2 sin(phi) angular part. This is the sum of i (exp(i phi) - exp(-i phi)), so that the particle is in a superposition of states, in one of which it "feels" a quadratic potential to its left (at z=-b) while in the other, one on its right (at z=b). Time evolution is a superposition of the time evolutions of each of the above states separately: the initial gaussian splits into two, each oscillating around the center of the potential it feels.

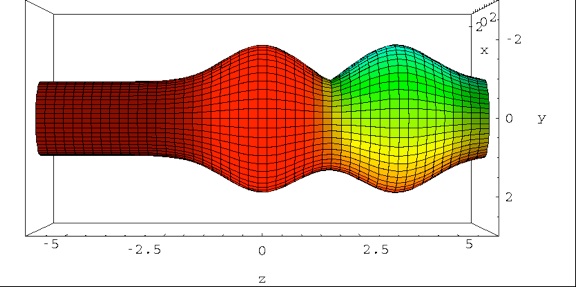
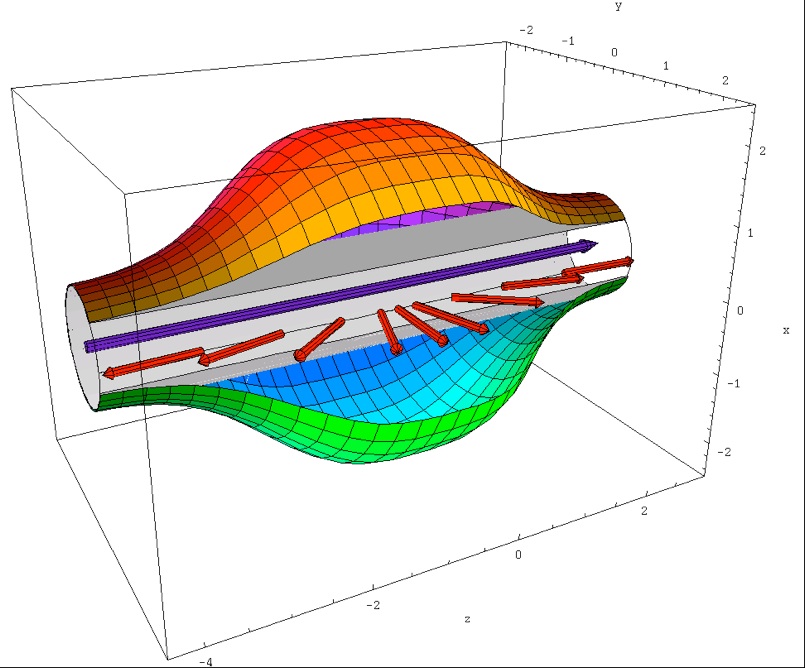
Notice that, in the above animation, each of the two gaussians oscillates between the center and one of the two extremes of the cylinder, although it looks as if they go through each other. Generalize the above to the case where the angular part of the initial wavefunction is a general function f(phi), with Fourier decomposition given by f(phi)=Sum(f_k exp(i k phi). The initial gaussian will then split in an infinite, in general, number of gaussians, one for each Fourier component, each of which will oscillate around the potential it feels. In the following animation we take f(phi)=1 + exp(-i phi) + 1.5 exp(-i 2 phi) + exp(- i 3 phi).

It is clear that the system works as a quantum Fourier transformer. Looking at the form of the wavefunction half a period after letting it go, when the gaussians have separated, one deduces the Fourier content of the initial f(phi) by looking at their relative amplitudes. In our animations, the relative phase can also be inferred by the color of each gaussian, at phi=0, at the above instant in time. Consider for example the initial superposition f(phi)=1+i exp(i phi). After half a period, viewed from the positive x-axis (i.e., from above, in the previous animations) it looks like

The relative phase difference of 90 degrees between the two Fourier components can be read off as the angular distance (in the color wheel) of the colors of the two gaussians at phi=0. (In the example shown above, phi=0 is the horizontal line in the middle of the figure. The gaussian on the left is red while the one on the right is green there. The two colors are 90 degrees apart in the color wheel, which agrees with the relative complex phase of the two components.)

When spin 1/2 is included, a perturbative treatment shows that the zeroth order (in the magnetic moment of the particle) hamiltonian eigenstates are the sum and difference of neighboring, same n SHO eigenstates, located at z=-k b and z=-(k+1) b (with angular part as before). We show below the symmetric ground state, for k=0, and the corresponding spin configuration, along the line phi=90 degrees. On the rest of the cylinder, the spin configuration is obtained simply by rotating the one shown. The color coded phase is the sum of the phases of the two spin components --- their difference can be inferred from the spin orientation.

When higher order corrections are taken into account, the spins cross the z-axis at a finite z and acquire a small negative radial component from that point to infinity. They get aligned asymptotically with the axis without ever leaving the radial plane. The effect is visually minuscule, even for values of the perturbation parameter of the order of unity. Recursive analytic expressions for the corrections to all states, at all orders, are given in the above mentioned article.