Algunas implicaciones filosóficas de las limitaciones de teorías de conjuntos ingenuas basadas en lógicas no clásicas
Morgan Thomas mostró recientemente que una familia de teorías de conjuntos ingenuas basadas en la lógica paraconsistente LP y otras lógicas relacionadas sufren de serias limitaciones expresivas. A primera vista, los resultados de Thomas parecerían un serio inconveniente para el desarrollo de matemáticas inconsistentes, pues esas teorías de conjuntos o bien carecen incluso de los conceptos más elementales necesarios para expresar las nociones básicas de la matemática clásica o bien son casi triviales. Thomas tiene toda la precaución de no sacar conclusiones tan fuertes acerca de la posibilidad de la matemática inconsistente, pero de todos modos están sugeridas en su trabajo y no pocos lectores podrían dar el salto hacia ellas. En esta plática argumentaré que resultados como los de Thomas deberían motivar más bien un rol diferente, no fundacional, para las teorías de conjuntos en las matemáticas no clásicas.
Algoritmos de Búsquedas por Similitud
Muchas aplicaciones modernas (i.e. reconocimiento de patrones o recuperación de información) requieren sistemas de búsquedas para encontrar a los objetos relevantes ante una consulta. En estas aplicaciones el patrón es el mismo, se tienen bases de datos enormes donde la búsqueda secuencial es impensable por el alto costo que podría implicar la comparación de 2 objetos de esa base. Este problema puede ser trasladado a un espacio métrico donde se tiene un universo de objetos y una medida de comparación entre ellos. En esta platica se mostrarán algunos algoritmos en este tema, además se mostrarán algunos avances de un sistema de foto-identificación de animales silvestres con técnicas no intrusivas.
Familias casi ajenas
Una familia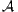 
⊆
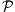(ω) es una familia casi ajena si para cualesquiera A,B ∈ 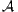distintos, se tiene que A ∩ B es finito. Las familias casi ajenas y casi ajenas maximales han sido extensamente estudiadas en los últimos años, pues juegan un papel importante en combinatoria infinita, en invariantes cardinales del continuo, ideales sobre ω y en otros temas de teoría de conjuntos.Dada una familia casi ajena 
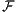, ¿cómo son las familias casi ajenas maximales que extienden a 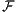y cuál es su cardinalidad mínima? Dado un ideal 
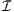sobre ω ¿cuál es la mínima cardinalidad de una familia casi ajena contenida en 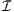? En esta plática abordaremos éstas y otras cuestiones sobre familias casi ajenas.
Un vistazo a las matemáticas formalizadas
El término matemáticas formalizadas se refiere al desarrollo de teoremas y demostraciones en un lenguaje formal de manera que un programa de computadora, llamado asistente de pruebas, pueda verificar mecanicamente todos los pasos de una demostración, certificando así que dicha prueba es correcta. En esta charla discutimos brevemente la necesidad de las matemáticas formalizadas en la actualidad, así como algunos aspectos lógicos detras del funcionamiento de los asistentes de prueba. Para esto nos serviremos de ejemplos sencillos desarrollados en el asistente de pruebas Coq (http://coq.inria.fr)
La Teoria de Ramsey y los espacios de Banach
La teoria de Ramsey ha motivado varios avances modernos en la teoria de espacios de Banach Separables. Hablaremos de algunos ejemplos de esto, entre los cuales están el Teorema de Brunel-Sucheston, que permite encontrar una subsucesion asintoticamente estable en fragmentos finitos de una sucesión normada de vectores arbitraria y algunos avances recientes en este ámbito. También discutiremos el concepto de distorsión en la esfera de un espacio de Banach y su relación con teoremas Ramsey-teóricos tales como el Teorema c0 de Gowers, el cual que extiende el conocido resultado de Hindman sobre la existencia, en una coloracion arbitraria de los naturales, de subconjuntos infinitos tales que todas sus sumas son del mismo color.