Se dice que una función $\color{blue}{f(x)}$ es continua en un punto $\color{red}{x_{0}}$ de su dominio, cuando
Esto significa, que los puntos "cercanos" a $\color{red}{x_{0}}$ son mandados por $\color{blue}{f}$ cerca de $\color{blue}{f(}$$\color{red}{x_{0}}$$\color{blue}{)}$
Se dice que $\color{blue}{f}$ es continua cuando $\color{blue}{f}$ es continua en cada uno de los puntos de su
$$\bbox[5px,yellow, border:2px solid red]{\lim_{x\rightarrow \color{red}{x_{0}}}\color{blue}{f(x)}=\color{blue}{f(}\color{red}{x_{0}}\color{blue}{)}}$$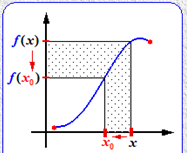

Esto significa, que los puntos "cercanos" a $\color{red}{x_{0}}$ son mandados por $\color{blue}{f}$ cerca de $\color{blue}{f(}$$\color{red}{x_{0}}$$\color{blue}{)}$
Se dice que $\color{blue}{f}$ es continua cuando $\color{blue}{f}$ es continua en cada uno de los puntos de su
$$\bbox[5px,yellow,border:2px solid red]{dominio}$$

8 Junio 2016, Creado con GeoGebra


